Top-Beiträge
Lifestyle
Baumentaster im Überblick: Alles, was ihr über die Wahl und Anwendung wissen müsst
Kurzzusammenfassung Was ist ein Baumentaster?Ein Baumentaster ist ein spezialisiertes Werkzeug, das den Baumschnitt in großer Höhe ermöglicht. Er dient vor allem dazu, Äste sicher und effizient zu entfernen, ohne eine Leiter nutzen zu müssen. Arten…
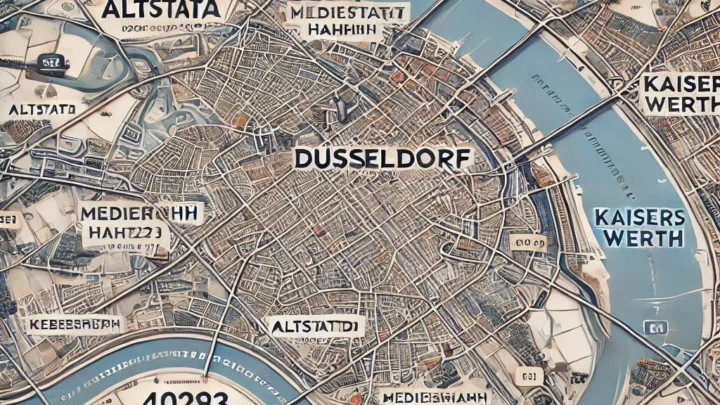
Postleitzahlen in Düsseldorf: So sind sie aufgebaut und das müsst ihr wissen
Kurzzusammenfassung Struktur der Postleitzahlen in DüsseldorfDie Postleitzahlen Düsseldorfs folgen einer klaren Struktur, die die Stadt in verschiedene Bereiche gliedert. Jede PLZ beginnt mit 40 und deckt bestimmte Stadtteile ab. Zentrale und bedeutende PLZDie Altstadt hat…
Gesundheit
Pica-Syndrom bei Katzen: Ursachen, Risiken und wie ihr helfen könnt
Katzen sind für ihre Neugier bekannt, doch manchmal wird diese zum Problem – besonders, wenn sie anfangen, unverdauliche Materialien wie Plastik, Stoff oder Papier zu fressen. Dieses Verhalten wird als Pica-Syndrom bezeichnet, eine Verhaltensstörung, die…
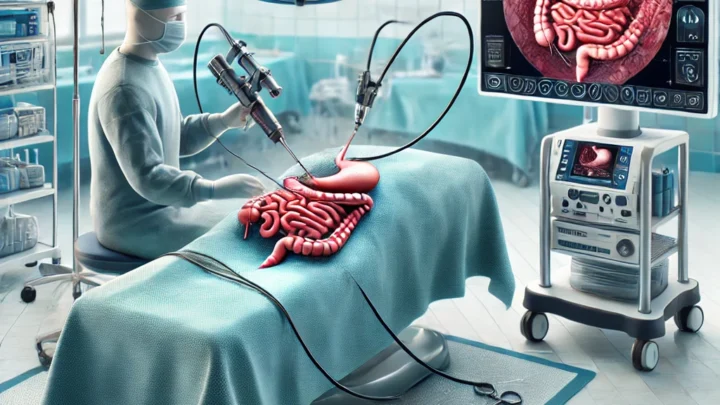
Viszeralchirurgie: Alles über die operative Behandlung der inneren Organe
Die Viszeralchirurgie, oft auch als Bauchchirurgie bezeichnet, ist ein faszinierendes und äußerst wichtiges Fachgebiet der Medizin. Es widmet sich der operativen Behandlung der inneren Organe des Bauchraums, darunter Magen, Darm und Leber. Mit modernen Verfahren,…
Familie
Kevin Trapp und Izabel Goulart: Liebe, Karriere und mögliche Familienpläne – Alles, was ihr wissen müsst
Kurzzusammenfassung Kevin Trapp – Ein Torwartstar aus DeutschlandKevin Trapp ist einer der bekanntesten deutschen Torhüter, der sowohl in der Bundesliga als auch international Erfolge feierte. Er ist ein fester Bestandteil der deutschen Nationalmannschaft. Ein Traumpaar:…
Kleine Hunderassen, die nicht wachsen: Die perfekten Begleiter für euer Zuhause
Kurzzusammenfassung Kleine Hunderassen sind platzsparend, pflegeleicht und eignen sich ideal für Stadtwohnungen oder kleinere Haushalte. Die Top 5 Mini-Hunderassen wie Chihuahua, Zwergspitz und Yorkshire Terrier bleiben klein und sind perfekte Begleiter für Singles, Familien und…
Reisen & Freizeit
Auszeit in Südtirol: Familienurlaub in Eppan an der Weinstraße
Euer Alltag ist oft bis zum Bersten gefüllt – Termine, Erledigungen und Verpflichtungen lassen nur wenig Raum für Ruhe und Erholung. Besonders als Familie spürt ihr diesen Druck stark, denn neben dem Job fordert auch…
Weihnachten in Dänemark: Ein Wintermärchen voller Tradition und Hygge
Ein einzigartiges Erlebnis, das Tradition, Gemütlichkeit und festliche Stimmung vereint, ist die Weihnachtszeit in Dänemark. Von alten Bräuchen bis hin zu modernen Weihnachtsmärkten – die dänische Art, diese besinnliche Zeit zu feiern, ist geprägt von…
Geld
Zweitwohnungssteuer legal umgehen: Diese Tipps sparen euch bares Geld
Kurzzusammenfassung: Grundlagen der Zweitwohnungssteuer: Die Zweitwohnungssteuer betrifft alle, die eine Nebenwohnung in einer anderen Gemeinde als ihrem Hauptwohnsitz nutzen. Legale Möglichkeiten zur Steuerreduktion: Durch eine Ummeldung zum Hauptwohnsitz oder berufliche Steuerbefreiung lässt sich die Steuer…
So funktioniert die Auszahlung von Guthaben bei Otto
Kurzzusammenfassung Die Auszahlung des Guthabens bei Otto erfolgt auf Antrag und kann unter bestimmten Voraussetzungen, wie zum Beispiel nach Rücksendungen, initiiert werden. Es gibt einen wichtigen Unterschied zwischen einer Gutschrift und einer Auszahlung – eine…